Heron of Alexandria | |
|---|---|
| Ἥρων | |
 17th-century German depiction of Heron | |
| Citizenship | Alexandria, Roman Egypt |
| Known for | Aeolipile Heron's fountain Heron's formula Vending machine |
| Scientific career | |
| Fields | Mathematics Physics Pneumatic and hydraulic engineering |
Hero of Alexandria (/ˈhɪəroʊ/; Greek: Ἥρων ὁ Ἀλεξανδρεύς, Hērōn hò Alexandreús, also known as Heron of Alexandria /ˈhɛrən/; fl. 60 AD) was a Greek mathematician and engineer who was active in Alexandria in Egypt during the Roman era. He has been described as the greatest experimentalist of antiquity and his work is representative of the Hellenistic scientific tradition.
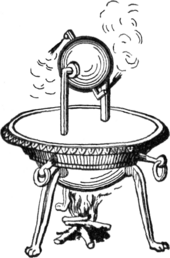
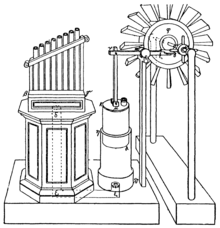
Hero published a well-recognized description of a steam-powered device called an aeolipile (sometimes called a "Hero engine"). Among his most famous inventions was a windwheel, constituting the earliest instance of wind harnessing on land. He is said to have been a follower of the atomists. In his work Mechanics, he described pantographs. Some of his ideas were derived from the works of Ctesibius.
In mathematics he is mostly remembered for Heron's formula, a way to calculate the area of a triangle using only the lengths of its sides.
Much of Hero's original writings and designs have been lost, but some of his works were preserved including in manuscripts from the Eastern Roman Empire and to a lesser extent, in Latin or Arabic translations.